Tradução do artigo do filósofo Gottfried Wilhelm Leibniz sobre o sistema binário
Tradução do artigo do filósofo Gottfried Wilhelm Leibniz "EXPLANATION OF BINARY ARITHMETIC".
Neste artigo de Leibniz, datado de 1703, têm-se as primeiras bases do que viria a ser o sistema binário.[ Hits: 2.970 ]
Por: Buckminster em 06/04/2024
EXPLICAÇÃO DA ARITMÉTICA BINÁRIA
Acredita-se que Leibniz foi o primeiro a utilizar o sistema binário em meados de 1700 (o artigo foi publicado em 1703), alguns dizem que Leibniz foi o inventor do sistema binário, porém, há controvérsias.
O que se sabe é que este artigo de Leibniz é o primeiro documento de que se tem notícia sobre o sistema binário como o conhecemos, onde o próprio Leibniz menciona as figuras chinesas de Fuxi datadas de mais de 4 mil anos atrás.
EXPLICAÇÃO DA ARITMÉTICA BINÁRIA QUE USA APENAS OS CARACTERES 0 E 1 COM ALGUMAS OBSERVAÇÕES SOBRE SUA UTILIDADE E SOBRE A LUZ QUE LANÇA SOBRE AS ANTIGAS FIGURAS CHINESAS DE FUXI
O cálculo normal da aritmética é feito de acordo com a progressão de dezenas. São usados dez caracteres, que são 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, que significam zero, um e os números sucessivos até nove, inclusive. E então, ao chegar a dez, recomeça-se escrevendo dez (10); dez vezes dez ou cem (100); dez vezes cem ou mil (1000); dez vezes mil ou 10 mil (10000) e assim por diante.

Mas em vez da progressão de dezenas, durante muitos anos usei a progressão mais simples de todas, que procede de dois em dois, tendo descoberto que é útil para o aperfeiçoamento da ciência dos números. Assim não utilizo outros caracteres exceto 0 e 1 e ao chegar a dois, começo de novo. É por isso que dois é aqui expresso por "10" e duas vezes dois, ou quatro, por "100", duas vezes quatro, ou oito, por "1000", duas vezes oito, ou dezesseis, por "10000", e assim por diante. Veja a Tabela de Números que pode ser estendida até onde for desejado.
Um olhar torna evidente a razão de uma célebre propriedade da progressão geométrica por dois em números inteiros, propriedade esta que sustenta que se tivermos apenas um desses números para cada grau podemos compor a partir deles todos os outros números inteiros abaixo do duplo do mais alto grau.
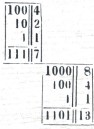
Pois aqui é como se disséssemos, por exemplo, que 111, ou 7, é a soma de quatro, dois e um, e que 1101, ou 13, é a soma de oito, quatro e um. Esta propriedade permite aos avaliadores pesar todos os tipos de massas com poucos pesos e pode servir na cunhagem para fornecer vários valores com poucas moedas. Estabelecer esta expressão de números nos permite realizar com muita facilidade todo tipo de operações.

E todas essas operações são tão fáceis que não haveria necessidade de adivinhar ou experimentar nada, como tem de ser feito na divisão comum. Não haveria mais necessidade de aprender nada de cor como acontece no cálculo comum onde é preciso decorar, por exemplo, que 6 e 7 juntos são 13 e que 5 multiplicado por 3 dá 15 de acordo com a Tabela "um vezes um é um" que é chamada Pitagórica(1). Mas aqui, tudo isso é encontrado e provado a partir da fonte, como fica claro nos exemplos anteriores sob os sinais meia-lua e círculo com ponto.
Contudo, não estou de forma alguma recomendando esta forma de contar a fim de introduzi-la no lugar da prática comum de contar até dez. Pois, além de estarmos acostumados com isso, não temos necessidade de decorar o que já aprendemos. A prática de contar até dez é mais curta e os números não são tão longos. E se estivéssemos acostumados a avançar por doze ou dezesseis, haveria ainda mais vantagem. Mas o cálculo por dois, isto é, por 0 e 1, como compensação pelo seu comprimento, é a forma mais fundamental de cálculo para a ciência e oferece novas descobertas que são então consideradas úteis, mesmo para a prática de números e especialmente para geometria.
A razão para isto é que, à medida que os números são reduzidos aos princípios mais simples, como 0 e 1, uma ordem maravilhosa torna-se aparente em todo o processo. Por exemplo, na própria Tabela dos Números fica claro em cada coluna que ela é regida por ciclos que sempre recomeçam. Na primeira coluna é 01, na segunda 0011, na terceira 00001111, na quarta 0000000011111111 e assim por diante. E pequenos zeros foram colocados na tabela para preencher a lacuna no início da coluna e para enfatizar melhor esses ciclos. Além disso, foram traçadas linhas dentro da tabela, o que mostra que o que está contido nas linhas sempre ocorre novamente abaixo delas. E acontece ainda que números quadrados, números cúbicos e outras potências, também números triangulares, números piramidais e outros números de figuras têm ciclos semelhantes de modo que as tabelas deles podem ser escritas imediatamente sem qualquer cálculo. E esta tarefa, demorada no início, mas que então fornece os meios para tornar o cálculo econômico e prosseguir até o infinito por meio de regras é infinitamente vantajosa.
O que é surpreendente neste cálculo é que esta aritmética de 0 e 1 contém o mistério das linhas de um antigo rei e filósofo chamado Fuxi(2), que se acredita ter vivido há mais de 4.000 anos e a quem os chineses consideram como o fundador de seu império e de suas ciências. Existem várias figuras lineares que lhe são atribuídas, todas elas remontando a esta aritmética, mas basta dar aqui a "Figura das Oito Cova", como é chamada, que se diz fundamental, e juntar a elas a explicação que é óbvia, desde que se note, em primeiro lugar, que uma linha inteira (-) significa unidade, ou 1, e em segundo lugar, que uma linha quebrada (--) significa zero, ou 0.

Os Chineses perderam o significado de "Cova" ou "Lineações de Fuxi" talvez há mais de mil anos e escreveram comentários sobre o assunto em que procuraram não sei que significados distantes, de modo que a sua verdadeira explicação vêm dos europeus. Eis como: há pouco mais de dois anos enviei ao Reverendo Padre Bouvet(3), célebre jesuíta francês que vive em Pequim, o meu método de contar por 0 e 1 e nada mais foi necessário para fazê-lo reconhecer que meu método foi a chave que o lembrou das figuras de Fuxi. Escrevendo-me em 14 de novembro de 1701, enviou-me a grande figura deste príncipe filosófico, que vai até 64, e não deixa mais margem para duvidar da veracidade da nossa interpretação de modo que se pode dizer que este Padre decifrou o enigma de Fuxi com a ajuda do que eu havia comunicado a ele. E como estas figuras são talvez o mais antigo monumento da ciência que existe no mundo, esta restituição do seu significado após tão grande intervalo de tempo parecerá ainda mais curiosa.
A concordância entre os números de Fuxi e minha Tabela de Números é mais óbvia quando os zeros iniciais são fornecidos na Tabela; parecem supérfluos, mas são úteis para mostrar melhor os ciclos da coluna, assim como lhes forneci pequenos anéis para distingui-los dos zeros necessários. E este acordo deixa-me com uma opinião elevada sobre a profundidade das meditações de Fuxi, uma vez que o que nos parece fácil agora não o foi naqueles tempos distantes. A aritmética binária ou diádica é, com efeito, muito fácil hoje em dia, exigindo pouca reflexão uma vez que é grandemente auxiliada pelo nosso modo de contar, do qual, ao que parece, apenas o excesso é removido. Mas esta aritmética comum por dezenas não parece muito antiga e pelo menos os Gregos e os Romanos a ignoravam e foram privados de suas vantagens. Parece que a Europa deve a sua introdução a Gerbert, que se tornou Papa sob o nome de Silvestre II(4), que a herdou dos Mouros da Espanha.
Ora, como se acredita na China que Fuxi é mesmo o autor dos caracteres chineses, embora estes tenham sido muito alterados em épocas posteriores, o seu ensaio sobre aritmética leva-nos a concluir que algo considerável poderia mesmo ser encontrado nestes caracteres no que diz respeito aos números e ideias se alguém pudesse descobrir os fundamentos da escrita chinesa, tanto mais que se acredita na China que ele teve consideração pelos números ao estabelecê-los. O Reverendo Padre Bouvet está fortemente inclinado a insistir neste ponto e é muito capaz de o conseguir de várias maneiras. No entanto, não sei se alguma vez houve uma vantagem nesta escrita Chinesa semelhante àquela que necessariamente tem de haver no projeto da Característica I que é que todo raciocínio derivável de noções poderia ser derivado dos caracteres dessas noções por uma forma de cálculo que seria um dos meios mais importantes de ajudar a mente humana.
NOTAS:
1. Leibniz está aqui se referindo à tabuada de multiplicação (Tabuada).
2. Uma figura mitológica, que se diz ter vivido no terceiro milênio a.C.
3. Joachim Bouvet (1656-1730), um missionário jesuíta francês que passou a maior parte da sua vida adulta na China. Ele e Leibniz corresponderam-se entre 1697 e 1707.
4. No seu “Discurso sobre a teologia natural dos chineses” (1716), Leibniz repetiu a sua afirmação de que Gerbert (ou seja, Gerbert d'Aurillac), que foi papa de 999 a 1003, introduziu o sistema decimal para a Europa cristã. Veja Leibniz, Writings on China , trad. e Ed. Daniel J. Cook e Henry Rosemont Jr. (Chicago: Tribunal Aberto, 1994), p135. A afirmação de Leibniz está errada; embora se acredite tradicionalmente que Gerbert introduziu os algarismos arábicos na Europa cristã, ele não introduziu o sistema decimal.
https://www.leibniz-translations.com/binary.htm
Compilando kernel no Debian Squeeze
Entendendo o que é URI, URL, URN e conhecendo as diferenças entre POST e GET
Encapsulando BIND 9 e Apache 2 para obter maior segurança
Como agendar um backup automático do PostgreSQL no Cron evitando o problema de senha
E a guerra contra bots continua
Como gerar um podcast a partir de um livro em PDF
Docalysis: Análise de Documentos com Inteligência Artificial
O Horizonte do Trabalho na Era dos Comandos: Uma Reflexão Necessária
Adicionando Legendas em Vídeo de forma automática por Reconhecimento Automático de Fala
Muito interessante.
Dá vontade de ler outros materiais do Leibniz.
Leibniz era extremamente inteligente e atento. Bem antes de S. Freud, vislumbrou o inconsciente (psíquico) no contexto de sistema. abraços!
Esse artigo é muito bom mesmo.
______________________________________________________________________
Inscreva-se no meu Canal: https://www.youtube.com/@LinuxDicasPro
Repositório GitHub do Canal: https://github.com/LinuxDicasPro
Grupo do Telegram: https://t.me/LinuxDicasPro
Meu GitHub Pessoal: https://github.com/mxnt10
Patrocínio
Destaques
Artigos
A combinação de WMs com compositores feitos por fora
Audacious, VLC e QMMP - que saudades do XMMS
SUNO OpenSource: Crie um servidor de gerador de música com IA
Instalação Completa e Configuração Básica do Void Linux
A Fundação da Confiança Digital: A Importância Estratégica de uma PKI CA na Segurança de Dados
Dicas
Instalar o Microsoft Teams no Ubuntu e Derivados
Script para configurar o DOOM Retro no Linux
Script para organizar janelas em cascata no KDE Plasma 6 (Wayland)
Tópicos
Erro ao baixar progamas no terminal (1)
Instalador não reconhece SSD Sata. (8)
Top 10 do mês
-

Xerxes
1° lugar - 127.533 pts -

Fábio Berbert de Paula
2° lugar - 59.599 pts -

Buckminster
3° lugar - 36.122 pts -

Alberto Federman Neto.
4° lugar - 25.592 pts -

Alessandro de Oliveira Faria (A.K.A. CABELO)
5° lugar - 19.735 pts -

Sidnei Serra
6° lugar - 19.628 pts -

Daniel Lara Souza
7° lugar - 19.001 pts -

Mauricio Ferrari (LinuxProativo)
8° lugar - 18.950 pts -

edps
9° lugar - 17.755 pts -

Andre (pinduvoz)
10° lugar - 14.399 pts




